<center> Operator Overloading in Python === *Written by [Alejandro](https://twitter.com/asanchezyali). Published 2021-06-15 on the [Monadical blog](https://monadical.com/blog.html).* </center> Python is an object-oriented programming language and one of its features is that it supports operator overloading, that is, it allows us to redefine the behavior of native operators (`+`,`-`, `*`, `/`, `+=`, `-=`, `**`, etc.).[<sup>1](#10) This means we can create code with greater readability, since we use native operators to define new representations, comparisons, and operations between objects that we have created. To illustrate how operator overloading works, I’ll walk you through how to redefine the behavior of the `+` and `-` operators using the special `__add__` and `__sub__` methods of Python classes. ## Using operator overloading The best way to understand an idea like this is to see it in practice. So, let’s start with an exercise which makes it necessary to redefine the behavior of Python's `+` and `-` operators. 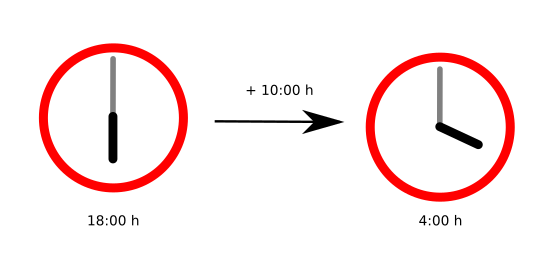Let’s say that we have a 24-hour clock, and we need to know what time the clock will show in 10 hours’ time. For example, if it’s now 18:00 in the evening, 10 hours later the clock will indicate that it’s 4:00 in the morning--18:00 hours + 10:00 hours = 4:00 hours. So, the summation of 24-clock-time is not like the usual summation of natural numbers, integers, or real numbers. <center>  </center> The aim of this exercise is to understand how the behavior of the addition and subtraction operators (`+`, `-`) can be redefined to properly capture clock arithmetic, so that "clock time” (in hours) can be added and subtracted to give appropriate results. Let’s get started. Initially, we are going to have a class called `Clock` in which we will represent the time with the format HH:MM: ```python class Clock: def __init__(self, time: str): self.hour, self.min = [int(i) for i in time.split(':')] def __repr__(self) -> str: min = '0' + str(self.min) return str(self.hour) + ':' + min[-2:] ``` Note that we are expecting the user to enter the `time` variable as a string in the format HH:MM. We have also made use of the `__repr__` method to define the console representation of our class, again in the format HH:MM. Let’s instantiate and execute it: ```python time_1 = Clock('10:30') time_1 ``` The console output will be: ```shell 10:30 ``` Now we can create two instances of the `Clock` class: ```python time_1 = Clock('10:30') time_2 = Clock('19:45') ``` If we try at this point to add these instances, we find the following error: ```python time_1 + time_2 --------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-17-9693c7986cbd> in <module>() ----> 1 time_1 + time_2 TypeError: unsupported operand type(s) for +: 'Clock' and 'Clock' ``` The problem here is that the `+` operator does not understand the operands of the `Clock` class. We can correct this error by adding a method associated with addition to the `Clock` class. In Python, this method is called `__add__` and requires two parameters. The first, `self`, is always required, and the second, `other`, represents another instance of the class itself. For example, `a.__add__(b)` will ask the `Clock object a` to add the `Clock object b` to itself. This can be written in the standard notation, `a + b`. For our case, the sum can be defined as follows: ```python def __add__(self, other: Clock) -> Clock: hour, min = divmod(self.min + other.min, 60) hour = (hour + self.hour + other.hour) % 24 return self.__class__(str(hour) + ':' + str(min)) ``` Notice how `divmod` is used here. This function performs a division--the same operation that we do with the division operator (`/`)--but it returns two values: the quotient and the residue. `divmod` converts the total number of minutes into the format HH:MM. The number of minutes is divided by 60 so that the quotient represents the hours and the residue represents the minutes. Since the clock uses the digits 0, 1, 2 ... 24 to represent hours, we calculate the total number of hours modulo 24. Finally, at the end the expression, `self.__class__(str(hour) + ':' + str(min))` is used to create a new instance of the `Clock` class so that the result can be reused in subsequent calculations. Let's make two instances of the `Clock` class: ```python time_1 = Clock('10:30') time_2 = Clock('19:45') ``` If we add them, we get: ```python time_1 + time_2 6:15 ``` This is exactly the result we want. Similarly, we can redefine the behavior of the (-) operator using the `__sub__` method: ```python def __sub__(self, other: Clock) -> Clock: hour, min = divmod(self.min - other.min, 60) hour = (hour + self.hour - other.hour) % 24 return self.__class__(str(hour) + ':' + str(min)) ``` We can do this in such a way that the final class will be: ```python Class Clock: def __init__(self, time): self.hour, self.min = [int(i) for i in time.split(':')] def __repr__(self) -> str: min = '0' + str(self.min) return str(self.hour) + ':' + min[-2:] def __add__(self, other: Clock) -> Clock: hour, min = divmod(self.min + other.min, 60) hour = (hour + self.hour + other.hour) % 24 return self.__class__(str(hour) + ':' + str(min)) def __sub__(self, other: Clock) -> Clock: hour, min = divmod(self.min - other.min, 60) hour = (hour + self.hour - other.hour) % 24 return self.__class__(str(hour) + ':' + str(min)) ``` It’s now possible to operate on `Clock` objects directly using the `+` and `-` operators, instead of calling methods: ```python time_1 = Clock('10:30') time_2 = Clock('19:45') time_3 = Clock('16:16') time_1 - time_2 + time_3 7:01 ``` ## Methods for overloading operators As we saw in the previous section, operator overloading allows us to redefine the behavior of arithmetic operators (`+`, `-`) and in fact, it can be done with any of Python's arithmetic, binary, comparison, and logical operators. We can use the following special methods to redefine any of the operators: | Operation | Syntax | Function | | -------- | -------- | -------- | | Addition | `a + b` | `add(a, b)` | | Concatenation | `seq1 + seq2` | `concat(seq1, seq2)`| | Containment Test | `obj in seq` | `contains(seq, obj)`| | Division | `a / b` | `truediv(a, b)`| | Division | `a // b` | `floordiv(a, b)`| | Division | `divmod(a, b)` | `divmod(a, b)` | | Bitwise And | `a & b` | `and_(a, b)` | | Bitwise Exclusive Or | `a ^ b` | `xor(a, b)` | | Bitwise Inversion | `~ a` | `invert(a)` | | Bitwise Or | `a | b` | `or_(a, b)` | | Exponentiation | `a ** b` | `pow(a, b)` | | Identity | `a is b` | `is_(a, b)` | | Identity | `a is not b` | `is_not(a, b)` | | Indexed Assignment | `obj[k] = v` | `setitem(obj, k, v)` | | Indexed Deletion | `del obj[k]` | `delitem(obj, k)` | | Indexing | `obj[k]` | `getitem(obj, k)` | | Left Shift | `a << b` | `lshift(a, b)` | | Modulo | `a % b` | `mod(a, b)` | | Multiplication | `a * b` | `mul(a, b)` | | Negation (Arithmetic) | `- a` | `neg(a)` | | Negation (Logical) | `not a` | `not_(a)` | | Positive | `+ a` | `pos(a)` | | Right Shift | `a >> b` | `rshift(a, b)` | | Slice Assignment | `seq[i:j] = values` | `setitem(seq, slice(i, j), values)` | | Slice Deletion | `del seq[i:j]`| `delitem(seq, slice(i, j))` | | Slicing | `seq[i:j]`| `getitem(seq, slice(i, j))` | | String Formatting | `s % obj`| `mod(s, obj)` | | Subtraction | `a - b`| `sub(a, b)` | | Truth Test | `obj`| `truth(obj)` | | Ordering | `a < b`| `lt(a, b)` | | Ordering | `a <= b`| `le(a, b)` | | Equality | `a == b`| `eq(a, b)` | | Difference | `a != b`| `ne(a, b)`| | Ordering | `a >= b`| `ge(a, b)` | | Ordering | `a > b`| `gt(a, b)` | *Source: [official python documentation](https://docs.python.org/3/library/operator.html)* Each object has several specialized methods that are used to interact with other objects or with native Python operators. Just like with the example of clock arithmetic, each of these methods can be implemented according to the following implementation scheme: ```python def __«operator»__(self, other: Object) -> Object: «instructions» return «output» ``` Here we need to select the «operator» and define the internal «instructions» and the «output» to customize its behavior. Overloading operators allows us to define new mathematical structures, such as cyclic groups, finite fields, vector spaces, groups, rings, and modules. There are useful applications for this in cryptography, discrete mathematics, and advanced calculus. Have a look through the [Python documentation](https://docs.python.org/3/reference/datamodel.html#special-method-names) to learn more about this topic and how the other operators can be overloaded. ## References 1. Python Data Model: https://docs.python.org/3/reference/datamodel.html#data-model 2. Special Method names: https://docs.python.org/3/reference/datamodel.html#special-method-names 3. Operators: https://docs.python.org/3/library/operator.html <a id="10">[1]</a> Not all languages support operator overloading. Though operator overloading can be more convenient and allow for more elegant code, it’s not essential for object-oriented programming. C, Java and Pascal do not suppose operator overloading. Python, C++, C#, Perl, and Ruby do support operator overloading. <center> <img src="https://monadical.com/static/logo-black.png" style="height: 80px"/><br/> Monadical.com | Full-Stack Consultancy *We build software that outlasts us* </center>